Многомерные адаптивные сплайны регрессии (MARSplines)

Поиск в справочнике по интернет-статистике

Многомерные адаптивные сплайны регрессии (MARSplines) - это реализация метода, предложенного Фридманом (1991) для реализации широкомасштабной регрессии, и она больше подходит для решения обеих задач регрессии (см., множественная регрессия ), а также классификации, в которых цель состоит в том, чтобы найти значение выходных (зависимых) переменных на основе входных (прогнозирующих) переменных. Существует много методов, подходящих для подгонки модели к количественным переменным, таких как линейная регрессия [например, Множественная регрессия , Общая линейная модель (GLM) ], нелинейная регрессия ( Поднятые линейные и нелинейные модели ) деревья регрессии (см. Деревья классификации и регрессии ) CHAID , Нейронные сети и т. д. (см. также Хасти, Тиширани и Фридман, 2001 г.).

Многомерные адаптивные сплайны регрессии ( MARSplines ) являются непараметрическими процедурами, не требующими функциональной зависимости между зависимыми и независимыми переменными. MARSplines моделирует отношения с помощью набора коэффициентов и базовых функций, «полученных» только из данных. Здесь используется стратегия, которую вы можете использовать, чтобы сказать «разделяй и стреляй». Ot, входное пространство разделено на области, в которых определены отдельные функции регрессии или классификации. Этот подход делает MARSplines особенно полезным с большим количеством измерений на входе (более двух переменных), когда, в случае других методов, он запускает проблему измерения.

Техника MARSplines особенно известна в данной области. Дата добычи из-за отсутствия необходимости предполагать что-либо типа отношений (линейных, логистических, ...) между зависимыми и независимыми переменными. Очень хорошие модели (дающие точные прогнозы) будут даны в ситуациях, когда зависимости очень сложны, немонотонны и трудны для любого параметрического моделирования. Подробнее об этом методе, а также о сравнениях с другими методами нелинейной регрессии (или деревьями регрессии) см. Hastie, Tibshirani and Friedman (2001).

Проблемы регрессии

В случае регрессии мы определяем взаимосвязь между набором количественных зависимых переменных (выходные данные, ответы) и набором независимых переменных (входные данные, прогноз). Таким образом, основываясь на знании значения входных переменных, мы хотим знать значение выходной переменной. Например, нас может интересовать количество дорожно-транспортных происшествий, причины которых (1) для погоды и (2) пьяный водитель. Это может выглядеть так:

Number_wypadkw = Staa + 0,5 * За_погода + 2,0 * Позиом_алко

Переменная Количество несчастных случаев является зависимой переменной, в зависимости от того, как мы видим (среди прочего) переменные Za_pogoda и Poziom_alkohol . Независимые переменные умножаются на числа 0,5 и 2,0 , которые являются коэффициентами регрессии. Чем выше коэффициент, тем сильнее влияние независимой переменной на зависимость переменной. Если обе предикторные переменные в этом (фиктивном) примере измеряются в одной и той же шкале (например, могут быть нормализованы до нулевого среднего значения и стандартного отклонения единицы), то из уравнения видно, что уровень алкоголя в четыре раза сильнее влияет на несчастные случаи, чем на послеуборочный . Если, с другой стороны, уровень алкоголя измеряется просто в профилях и Za_pogoda , например, в метрах видимости, то мы не можем сравнивать коэффициенты регрессии друг с другом.

Дополнительные подробности о подобных типах статистических моделей можно найти в главе Множественная регрессия или Общие линейные модели (GLM) как хорошо Общие регрессионные модели (ГРМ) , В целом, в социологии, в естествознании регрессионные процедуры применяются в очень широком диапазоне. Регрессия позволяет исследователю искать (и находить) ответ на вопрос о лучшем предикторе характеристики. Педагог, например, может искать лучшего предиктора успеха студента в университете. Психолог спросит, какая из черт личности позволяет наилучшим образом оценить социальную адаптацию человека. Может быть интересен социолог, который по многим социальным показателям позволит оценить, как новая группа иммигрантов адаптируется в новых условиях.

Многомерные адаптивные сплайны регрессии

Вышеупомянутый пример дорожно-транспортных происшествий будет типичным результатом использования линейной регрессии, где в качестве переменной отклика предполагается, что она линейно зависит от переменных прогнозирования. Линейная регрессия относится к параметрическим методам, в которых предполагается конкретная форма зависимости функции (например, линии), и только числовые параметры функции оцениваются на основе данных. В непараметрических методах (см., Например, непараметрические корреляции ) пока нет, нет причин для зависимости между переменными. Построение модели зависимости контролируется данными.

Многомерные адаптивные сплайны регрессии (MARSplines) - это непараметрические процедуры, которые не нуждаются в какой-либо функциональной зависимости от переменных, зависящих от независимых переменных. В MARSplines зависимость строится из коэффициентов и так называемых базовых функций, полностью определяемых данными. Общий механизм действия MARSplines можно представить как множественные линии регрессии линий (см. нелинейная оценка ). Пределы сегментов (определяемые на основе данных) определяют «диапазоны применимости» отдельных линейных линейных.

Основные функции. MARSplines использует двусторонние наклонные линейные функции (видимые для него) в качестве базовых функций для линейного / нелинейного приближения зависимостей между предикторными переменными и переменными отклика.

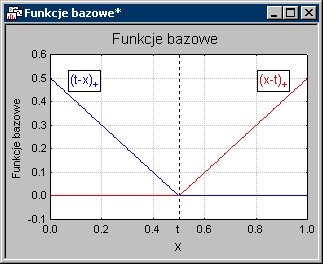
На приведенном выше рисунке показан простой пример двух основных функций (tx) + и (xt) + (по данным Hastie и др. 2001, рис. 9.9). Параметр t является базисной функцией (задающей «участки» линейной линейной регрессии); положение пятки (параметр t ) определяется данными. Отметки «+» после выражений (tx) и (xt) означают просто, что мы берем только положительную часть линейной функции. Вместо отрицательных значений принимается ноль, как видно на графике.

Модель MARSplines. Основные функции наряду с параметрами модели (найдены с помощью методы наименьших квадратов ) разрешить прогнозирование на основе входных переменных. Общее обоснование MARSplines (Hastie et al., 2001, R 9.19) дает:

где суммирование проходит через все M функциональных компонентов модели (более подробно о модели см. Технические примечания ). Таким образом, y вычисляется как функция прогнозирующих переменных X (и их взаимодействия). Элементами этой функции являются исходная строка ( 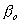) и взвешенные (веса 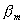) сумма одной или нескольких базовых функций 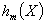такие, как показано на рисунке. В этой модели мы можем посмотреть на сумму базовых функций, выбранных из набора большого числа таких функций, охватывающего все значения каждого предиктора (в этом наборе у нас есть базовая функция и параметр t для каждого отдельного значения, каждого предиктора). Алгоритм MARSplines ищет пространство всех входных и прогностических значений (pooe vie t ), а также взаимодействие между переменными. Дополнительные базовые функции (выбранные из набора всех приемлемых функций) добавляются в модель таким образом, чтобы максимизировать общий уровень регулировки (путем минимальной суммы квадратов). Результатом этой операции является поиск наиболее важных независимых переменных и их наиболее важных взаимодействий. Подробности алгоритма см. Технические примечания или (Hastie et al 2001).

Предикторы качества. MARSplines адаптирован к задачам, в которых существуют как количественные, так и качественные прогнозные переменные. Однако базовый алгоритм MARSplines предполагает, что предикторы являются количественными, и, например, вычисляемую программу программа обычно не скажет с кодами классов переменных качества. Для получения подробной информации о переменных качества в MARSplines см. Фридман (1993).

Много зависимых (выходных) переменных. Алгоритм MARSplines можно использовать для многих выходных переменных. В таком случае с многомерным выходным сигналом алгоритм задает общий набор базовых функций для предикатов, но отдельный набор коэффициентов для каждой выходной переменной. Этот подход к многомерной выходной переменной похож на некоторые алгоритмы нейронные сети где множественный выход рассчитывается на основе общих нейронов; в MARSplines множественный вывод вычисляется из общих базовых функций с конкретными (для каждой выходной переменной) коэффициентами.

MARSplines и классификация. Поскольку MARSplines справляется с несколькими выходными переменными, его также легко применить к вопросам классификации. В этой ситуации MARSplines сначала кодирует качество выходной переменной, преобразовывая ее в многомерные индексные переменные (1 = регистр принадлежит классу k, 0 = регистр не принадлежит классу k), затем сопоставляет модель и вычисляет прогноз, а на последнем этапе присваивает регистры классу по самым высоким значениям прогнозирования (описание процедуры см. в Hastie, Tibshirani and Freedman 2001). Мы отмечаем, и это приложение дает эвристическую классификацию, которая может очень хорошо работать на практике, но вероятности классификации не создаются на основе статистической модели.

Как правило, непараметрические модели хорошо адаптируются к данным, очень гибки, что может привести к неблагоприятному явлению чрезмерная корректировка (переоснащение, переоснащение), если этому не противодействуют. Такие модели могут быть легко достигнуты на тренировочных данных (если разрешено достаточное количество параметров), но будут работать для новых данных (если знания, полученные из обучающих данных, не очень хорошо обобщены в модели). MARSplines , как и большинство этих методов, имеют тенденцию чрезмерно приспосабливаться к данным. Для борьбы с проблемой MARSplines использует технику обрезки, аналогичную зачистка (в деревьях классификации), ограничивая zoono модели, уменьшая количество основных функций.

MARSplines как метод выбора признаков (предикторов). Выбор наиболее важных и сокращение (удаление) наименее важных базовых функций - это операция, результат которой можно использовать для выбора соответствующих предикторов. Алгоритм MARSplines выберет только те базовые функции (то есть те переменные прогнозирования), которые дают «измеримый» ввод прогноза (более подробно см. Технические примечания ).

MARSplines обретет популярность, находя прогностические модели в «трудных» задачах интеллектуальный анализ данных то есть когда переменная зависимости не зависит от предиктора простым или, по меньшей мере, монотонным способом. В таких случаях модели могут альтернативно рассматриваться CHAID , Деревья классификации и регрессии или любая из многих архитектур нейронные сети , Из-за особого способа сопоставления предиктора для модели, он используется в MARSplines ( основные функции ), этот алгоритм работает из «хорошего» правила, в котором могут использоваться деревья регрессии, то есть когда иерархическое последовательное деление предикторов работает хорошо. Потому что вместо того, чтобы рассматривать эту технику как продвижение множественной регрессии (как это было во введении), вы можете рассматривать MARSplines как орошение для деревьев регрессии, в которых «жесткие» двоичные разбиения были заменены более загадочными базовыми функциями. Мы можем найти подробности в литературе: Асти, Тибширани и Фридман (2001).

Алгоритм MARSplines ( многовариантные адаптивные регрессионные сплайны ) представляет собой двухэтапную процедуру, применяемую последовательно и к данной модели. На первом этапе мы строим модель, то есть увеличиваем ее zoono (значительно), добавляя больше основные функции для достижения максимальной (определяемой пользователем) степени сложности. Затем начинается обратная процедура, удаляя наименее значимые базовые функции из модели, то есть те, которые удаляют наименее значимые соответствия модели (в смысле наименьших квадратов). Поэтому реализация алгоритма происходит в следующие шаги:

1. Запуск алгоритма по простейшей модели с функцией базы фиксированных значений.

2. Поиск для каждой переменной и возможных пяток пространства базовых функций и добавление к модели тех функций, которые максимизируют определенные показатели качества подбора модели (минимизация или прогноз).

3. Шаг 2 повторяется до тех пор, пока не будет достигнута максимальная сложность модели.

4. В конце модель с базовыми функциями обновляется, что дает вклад в улучшение качества модели (в смысле самые маленькие квадраты ).

Алгоритм MARSplines ( многовариантные адаптивные регрессионные сплайны ) строит модели из двусторонних уменьшенных предикторов (x) в следующей форме:

С этим основные функции с помощью линейного / нелинейного приближения можно смоделировать фактическое соотношение f (x) .

Модель MARSplines для зависимых переменных (выходных) y , имеющих M выражений, может быть записана следующим образом:

где суммирование проходит через все M компонентов модели, aboibm - это параметры модели (как и все остальные базовая функция , определяется по данным). Функция H определяется следующим образом:

где xv (k, m) - предиктор kw m-го произведения. Для строки взаимодействия K = 1 мы имеем аддитивную модель, для порядка K = 2 модель является интерактивной.

В пошаговой процедуре следующие базовые функции добавляются в модель до заданного максимального числа, которое должно быть достаточно большим (по крайней мере, в два раза больше оптимального, с точки зрения минимальных квадратов).

После применения алгоритма выбора базовых функций запускается обратная процедура, в которой модель выбрасывает базовые функции в порядке, обеспечивающем наименьшее улучшение соответствия модели (в смысле наименьших квадратов). Вычисляется функция ошибки наименьших квадратов (обратная подгонка). Мера соответствия является так называемой обобщенная перекрестная проверка, учитывающая не только остаточную, но и модель. Это дано:

где

в то время как N - число случаев в данных, d - эффективное количество степеней свободы, равное количеству независимых базовых функций. Параметр c управляет штрафом за добавление базовых функций. Опыт показывает, что лучший C получается при 2 <d <3 (см. Hastie et al., 2001).